Aufgabe A 2.1
In einem Labor wird erforscht, wie sich Bakterien unter verschiedenen Bedingungen entwickeln.
Betrachtet wird jeweils der Flächeninhalt der von den Bakterien eingenommenen Fläche.
Versuchsreihe 1
Bei ungehinderter Vermehrung wird der Flächeninhalt während der ersten zwölf Stunden beschrieben durch
die Funktion f mit f(t)=20·e0,1·t (t in Stunden nach Beobachtungsbeginn, f(t) in mm²).
a) Bestimmen Sie den Flächeninhalt drei Stunden nach Beobachtungsbeginn.
Berechnen Sie den Zeitpunkt, zu dem sich der Flächeninhalt im Vergleich zum Beobachtungsbeginn verdreifacht hat.
Berechnen Sie die momentane Änderungsrate des Flächeninhalts zwei Stunden nach Beobachtungsbeginn.
(3,5 VP)
b) Berechnen Sie
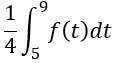.Interpretieren Sie das Ergebnis im Sachzusammenhang.
(3,5 VP)
Versuchsreihe 2
Wenn man einer Bakterienkultur ein Antibiotikum hinzugibt, dann wird der Flächeninhalt durch die
Funktion g beschrieben mit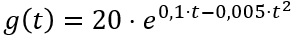
Die Abbildung zeigt den Graphen der Funktion g.
c) Der Flächeninhalt nimmt zu einem bestimmten Zeitpunkt seinen größten Wert an.
Berechnen Sie diesen Wert.
Berechnen Sie den Zeitpunkt, zu dem der Flächeninhalt wieder so groß ist, wie zu Beobachtungsbeginn.
(5 VP)
| Downloads |
PowerPoint